Понятие устойчивости линейных непрерывных сау
Система называется устойчивой, если:
1) после снятия воздействия по окончании переходного процесса система возвращается в исходное равновесное состояние;
2) после изменения воздействия на постоянную величину по окончании переходного процесса система приходит в новое равновестное состояние.
Определим условия устойчивости.
Выходная и входная величины в системе связаны с помощью дифференциального уравнения. Решение этого дифференциального уравнения при заданном значении входной величины представляет собой закон изменения выходной величины во времени. Но это решение состоит из двух составляющих:
x(t)=xв(t)+xсв(t),
где xв(t)- вынужденная составляющая, однозначно связанная с изменением входной величины. Она определяется как частное решение неоднородного дифференциального уравнения с правой частью;
xсв(t)- свободная составляющая, изменяющаяся во времени в течение переходного процесса.
Именно свободная составляющая и определяет переходной процесс в системе. Определяется она общим решением однородного дифференциального уравнения
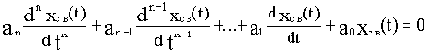
в виде суммы составляющих
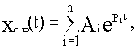
где Ai- постоянные интегрирования, определяющиеся начальными условиями;
Pi- корни характеристического уравнения.
Характеристическое уравнение составляется на основании исходного дифференциального уравнения:
anpn+an-1pn-1+...+a1p+a0=0
В общем случае корни являются комплексными. При этом они образуют пары сопряженных корней:
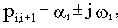
где

При этом, если
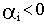
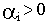
Отсюда следует, что общим условием затухания всех составляющих, а значит, и всего переходного процесса в целом является отрицательность действительных частей всех корней характеристического уравнения системы.
Если хотя бы один корень имеет положительную действительную часть, он даст расходящуюся составляющую переходного процесса и система будет неустойчивой.
Изображая корни характеристического уравнения системы точками на комплексной плоскости, как показано на рис.3.1, условие устойчивости можно сформулировать еще так: условием устойчивости САУ является расположение всех корней характеристического уравнения в левой комплексной полуплоскости.
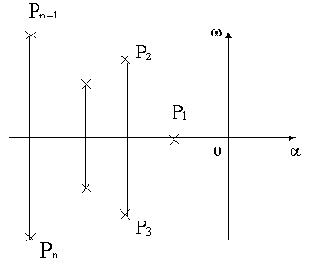
Рис.3.1
Мнимая ось

1) нулевым корнем p1=0;
2) парой чисто мнимых корней
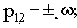
3) бесконечно удаленным корнем
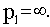
Бесконечность на комплексной плоскости рассматривается как бесконечно удаленная точка, противоположная нулевой. Поэтому она тоже является границей между правой и левой полуплоскостями.
Вычисление корней весьма просто лишь для характеристического уравнения первой и второй степени. Но ведь для определения устойчивости не нужно знать абсолютное значение корней, необходимо знать лишь, в какой полуплоскости они находятся. Поэтому важное значение приобретают правила, позволяющие определять устойчивость системы без вычисления корней. Эти правила называют критериями устойчивости.
К основным критериям устойчивости относятся алгебраический критерий Гурвица и частотные критерии Михайлова и Найквиста.
К содержанию