Минимально- и неминимально-фазовые звенья
Введем вначале понятия нулей и полюсов передаточной функции. Нулями передаточной функции
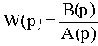
Звено называется минимально-фазовым, если все нули и полюса его передаточной функции имеют отрицательные или равные нулю вещественные части.
Звено называют неминимально-фазовым, если хотя бы один нуль или полюс его передаточной функции имеет положительную вещественную часть.
Все рассмотренные выше типовые звенья, кроме звена чистого запаздывания, являются минимально-фазовыми.
Возьмем в качестве примера неминимально-фазовое звено с передаточной функцией
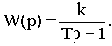
Такое звено можно получить, если охватить апериодическое звено с передаточной функцией W0(p)=k0/(T0p+1) положительной обратной связью с передаточной функцией W0c(p)=k0c Эквивалентная передаточная функция такого соединения будет
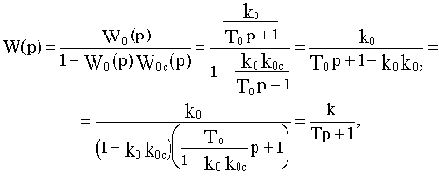
где

При k0k0c>1 параметры k и Т будут отрицательны, но если умножить и числитель, и знаменатель выведенной передаточной функции на минус единицу, то получим записанную выше передаточную функцию неминимально-фазового звена.
Эта передаточная функция имеет положительный полюс p1=1/T.
Частотные характеристики такого звена:
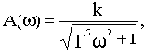
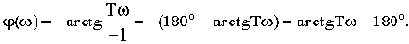
Но для обычного апериодического звена имеем:
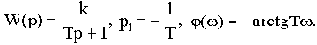
Разница между ними. как видим, в величине фазы. Амплитудные же характеристики одинаковы. Оказывается, что из всех возможных звеньев с одинаковыми амплитудными характеристиками обычные типовые звенья обладают наименьшими по абсолютному значению фазовыми характеристиками. В этом и состоит смысл введенных терминов.
Важным свойством минимально-фазовых звеньев является однозначное соответствие амплитудной и фазовой частотных характеристик. Другими словами, по заданной амплитудной характеристике можно определить фазовую и наоборот.
К содержанию