Критерий устойчивости гурвица
По этому критерию условия устойчивости сводятся к выполнению ряда неравенств, связывающих коэффициенты уравнения системы. Пусть характеристический полином САУ будет (характеристический полином определяет левую часть уравнения САУ, т.е. знаменатель передаточной функции):
A(p)=anpn+an-1pn-1+...+a1p+a0
Пологая an>0(если anотрицательно, то это условие можно выполнить, умножив весь полином на минус единицу), составляется из коэффициентов A(p)определитель Гурвица:

В первой строке пишутся коэффициенты с условно нечетными индексами (т.е. коэффициенты с индексами n минус нечетное число, где n - порядок характеристического полинома), во втором - с условно четными (т.е. n минус четное число). Концы строк заполняются нулями так, чтобы матрица имела n столбцов. Третья и четвертая строки получаются сдвигом первых двух на одно место вправо и т.д. ( всего строк - n).
Условия устойчивости заключаются в требовании положительности определителя Гурвица и всех его диагональных миноров. Из этого правила можно вывести более удобное для практического применения: САУ устойчива, если положительны все коэффициенты характеристического полинома и предпоследний диагональный минор определителя Гурвица (справедливо для систем не выше четвертого порядка).
Выведем выражение для расчета предпоследнего диагонального минора

Для систем третьего порядка (n=3):
A(p)=a3p3+a2p2+a1p+a0;
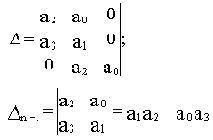
Для систем четвертого порядка (n=4):
A(p)= a4p4+a3p3+a2p2+a1p+a0;

Перед дальнейшим изложением материала уточним терминологию и покажем, как без излишних вычислений составляется характеристический полином замкнутой САУ по заданной структурной схеме. Для пояснений воспользуемся схемой на рис.3.2.
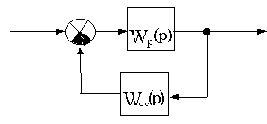
Рис.3.2
Пусть передаточная функция разомкунтой системы Wp(p) и цепи обратной связи Woc(p) будут:
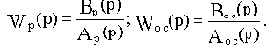
Последовательное соединение элементов с передаточными функциями Wp(p) и Woc(p) даст разомкнутую цепь звеньев замкнутой САУ с передаточной функцией Wр.ц.(p), которую будем называть передаточной функцией разомкнутой цепи:
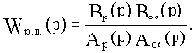
Через принятые обозначения определим передаточную функцию замкнутой САУ:
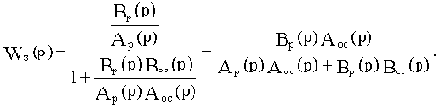
Отсюда характеристический полином замкнутой САУ будет:
Aз(p)=Ap(p)Aoc(p)+Bp(p)Boc(p).(3.3)
То есть, характеристический полином замкнутой САУ равен сумме числителя и знаменателя передаточной функции разомкнутой цепи.
В качестве примера рассмотрим САУ со структурной схемой, приведенной на рис.3.3, для которой необходимо определить соотношение параметров, обеспечивающих устойчивость.
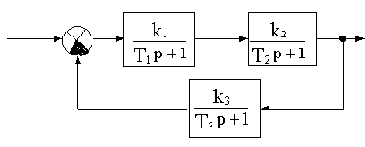
Рис.3.3
Составим характеристический полином замкнутой САУ в соотвествии с (3.3):
Aз(p)=(T1p+1)(T2p+1)(T3p+1)+k1k2k3.(3.4)
Запишем характеристический полином в общем виде:
Aз(p)=a3p3+a2p2+a1p+a0;
где
a3=T1T2T3, a2=T1T2+T2T3+T3T1,
a1=T1+T2+T3, a0=k1k2k3+1=k+1.
Условия устойчивости сводятся к следующим неравенствам:
T1T2T3>0, T1T2+T2T3+T3T1>0,
T1+T2+T3>0, k>0
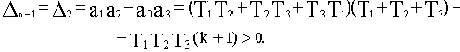
Первые три неравенства интереса не представляют, если мы ограничиваем рассмотрение положительными значениями постоянных времени. Четвертое неравенство показывает лишь, что в случае ошибки и включения вместо отрицательной связи положительной система станет неустойчивой.
Реальные ограничения на значения параметров системы накладывает последнее неравенство. Его удобнее записать в другом виде, поделив левую часть на T1T2T3:
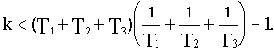
Это неравенство показывает, что устойчивость САУ в конце концов нарушится при неограниченном увеличении коэффициента передачи k при любых значениях постоянных времени.
Предельное по величине значение k, при котором САУ теряет устойчивость, принято называть критическим (или граничным). Для рассматриваемого примера:
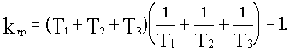
Значение граничного коэффициента передачи зависит не от абсолютных значений постоянных времени , а от их отношения.
Для рассмотренной здесь структуры при равенстве всех постоянных времени, преобразовав соотношение (3.5) к виду
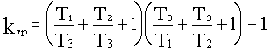
легко определить, что kгр=8. Для данной структуры найденное значение kгр является минимальным. Чем больше будут различаться постоянные времени, тем больше будет величина kгр.
С помощью критериев устойчивости можно строить области устойчивости.
При проектировании САУ ряд параметров и звеньев являются заданными, так как они определяются требованиями технологического процесса и конструктивными особенностями объекта регулирования. В то же время имеется несколько параметров, которые можно менять в определенных пределах. Для определения влияния значений каких-либо варьируемых параметров на устойчивость строят области устойчивости системы в пространстве этих варьируемых параметров.
Уравнения границ области устойчивости получаются из условий устойчивости, если заменить в них неравенства на равенства (это соответствует нахождению системы на границе устойчивости).
В общем случае границы области устойчивости по критерию Гурвица строятся по следующим уравнениям:
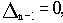
Первое уравнение соответствует наличию у характеристического уравнения пары сопряженных мнимых корней, второе равенство соответствует наличию нулевого корня, а третье - наличию бесконечного корня.
Для САУ, уже рассмотренной выше (см. рис.3.3), зададим варьируемыми параметрами общий коэффициент передачи разомкнутой цепи k и постоянную времени T1. Уравнениями для построения границ области устойчивости будут:
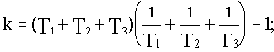
k+1=0;
T1=0.
Границы области устойчивости изображены на рис.3.4. Около границ принято наносить штриховку в сторону области устойчивости.
Каждая точка внутри области устойчивости определяет комбинацию варьируемых параметров k и T1, при которых система устойчива. Причем, если система в пространстве всех своих параметров не имеет области устойчивости, она называется структурно неустойчивой. Для получения устойчивости в этом случае необходимо изменить структуру.
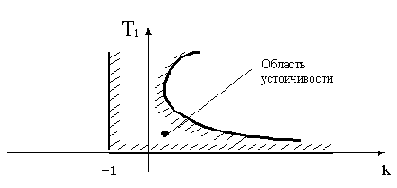
Рис.3.4
Пример 3.1.
Определить устойчивость САУ, структурная схема которой приведена на рис.3.5, воспользовавшись критерием устойчивости Гурвица.
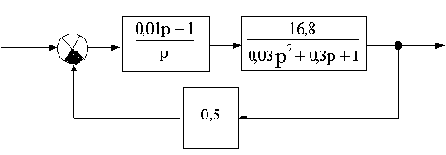
Рис.3.5
Для установления устойчивости определим граничное значение коэффициента передачи и сравним его с имеющимся значением коэффициента.
Передаточная функция разомкнутой цепи
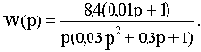
В соответствии с (3.3) характеристический полином замкнутой системы
Aз(p)=p(0,03p2+0,3p+1)+k(0,01p+1)=
=0,03p3+0,3p2+(1+0,01k)p+k=a3p3+a2p2+a1p+a0,
где a3=0,03; a2=0,3; a1=1+0,01k; a0=k.
Так как система имеет третий порядок, то она будет находится на границе устойчивости при равенстве нулю выражения (3.1):
a1a2-a0a3=0,3(1+0,01kгр)-0,03kгр=0
Отсюда находим kгр=11,1
Коэффициент передачи разомкнутой цепи k=8,4 меньше, чем kгр Следовательно, система в замкнутом состоянии устойчива.
К содержанию